딥러닝/논문리뷰

[논문리뷰] Generalized Intersection over Union: A Metric and A Loss for Bounding BoxRegression(GIoU)

참외맛메로나_ 2021. 2. 17. 20:49

0. Before review

이 논문은 Loss function의 파라미터 자체를 IoU로 변경하여 기존 딥러닝 네트워크의 추가적인 성능 향상을 목표로 한 논문이다. 19년 CVPR에서 소개된 논문임에도 불구하고 현재(21년 2월 17일) 기준 인용수가 366회에 달할 정도로 주목을 받은 논문이라고 할 수 있다.

 

논문에 대한 리뷰에 앞서, matlab에서 직접 작성한 GIOU를 계산하기 위한 코드를 첨부한다.

function [giou,iou] = gIoU(bboxes1, bboxes2)
    % Reference : Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression
    % Calculate generalized Intersection over Union
    
    % define point of first bounding boxes.
    x1p = bboxes1(:,1);
    x2p = bboxes1(:,1) + bboxes1(:,3);
    y1p = bboxes1(:,2);
    y2p = bboxes1(:,2) + bboxes1(:,4);
    
    % define point of second bounding boxes.
    x1g = bboxes2(:,1);
    x2g = bboxes2(:,1) + bboxes2(:,3);
    y1g = bboxes2(:,2);
    y2g = bboxes2(:,2) + bboxes2(:,4);
    
    % Calculate Area of Bboxes1&2
    area_1 = (x2p - x1p) .* (y2p - y1p);
    area_2 = (x2g - x1g) .* (y2g - y1g);
    
    %cal intersection
    IoU_min = bboxOverlapRatio(bboxes1,bboxes2, 'Min');
    Overlap = IoU_min .* min(area_1, area_2');
    All_Area = (max(x2p, x2g') - min(x1p,x1g')).*(max(y2p,y2g') - min(y1p,y1g'));
    C_boxes = (All_Area - (area_1+area_2'-Overlap))./All_Area;
    
    iou = bboxOverlapRatio(bboxes1, bboxes2);
    giou = iou - C_boxes;
end

Matlab에서 위의 코드로 GIoU를 계산할 수 있다.

1. Introduce

  2D 이미지 분야에서 딥러닝 네트워크를 학습 시킬 때 최종적인 목표는 Ground Truth를 Prediction이 완벽하게 추종하는 것이다. 즉, IoU(Intersection over union)이 1이 되는것을 목표로 한다. 하지만 대다수의 최신 네트워크들은 IoU를 향상시키기 위해서 x, y, w, h라는 파라미터를 활용한 학습을 진행한다. 하지만 ln loss를 최소화 하는 것과 IoU 값을 개선하는 것 사이에는 큰 관련이 없다는 문제가 존재한다.

각 케이스별 l2 loss/IoU/GIoU 비교

 위의 그림에서 두 상자의 좌측 하단 모서리를 고정하고, 검은 상자(여기서는 Prediction이라 가정하자)의 우측 상단 모서리가 회색 점선으로 그려진 원 위에 존재할 때, 모든 경우에서 l2 loss는 같다. 하지만 IoU와 GIoU는 다른 값을 갖고, 우리의 최종 목표인 완벽하게 포개지는 박스를 예측하는 것(IoU = 1)에도 영향을 주지 않는다.

각 케이스별 l1 loss/IoU/GIoU 비교

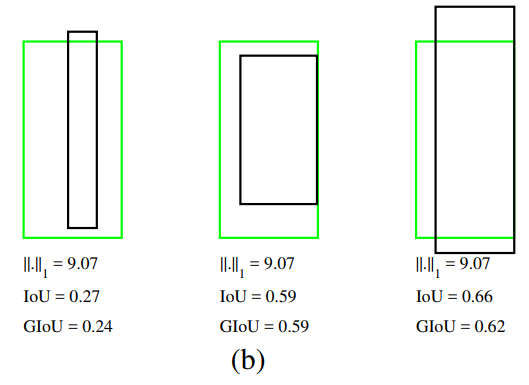
 그렇다면 l1 loss는 다를까? 딥러닝에선 잘 사용하지는 않지만(Overfitting의 위험성 등 때문) 이 경우에도 비교해보면 세 경우에서 l1 loss가 일정할 때, IoU와 GIoU가 다르게 계산된다.

 

 위와 같은 이유 때문에 저자는 여기서 IoU를 Loss function의 파라미터로서 도입했을 때 직접적인 성능 향상이 가능할 것이라고 예측했다.

2. Related works

 하지만 IoU를 훈련에 활용하기 앞서 문제가 있는데, 바로 박스가 떨어졌을 때 그 문제가 발생한다.

A: Ground Truth / B: Prediction

 그림에서 볼 수 있듯, 예측된 박스가 Ground Truth와 조금이라도 겹친 경우에는 훈련에 활용할 수 있지만, 겹치지 않은 경우 박스가 얼마나 떨어졌는지 판단할 근거가 존재하지 않는다. 즉, Loss = 1 - IoU로 훈련한다고 가정하면 박스가 떨어져있는 경우에는 Loss가 1이 되고 Gradient exploding이 발생할 것을 예측할 수 있다.

3. Generalized Intersection over Union

주저리주저리

 드디어 본론이다. 논문에서는 GIOU를 계산하는 알고리즘 두 가지(한 가지는 세부적인 설명)을 제시하며 주저리주저리 설명하지만 이를 간단히 그림으로 설명하면,

GIoU를 이해하기 쉽게 그림으로 표현해봤다.

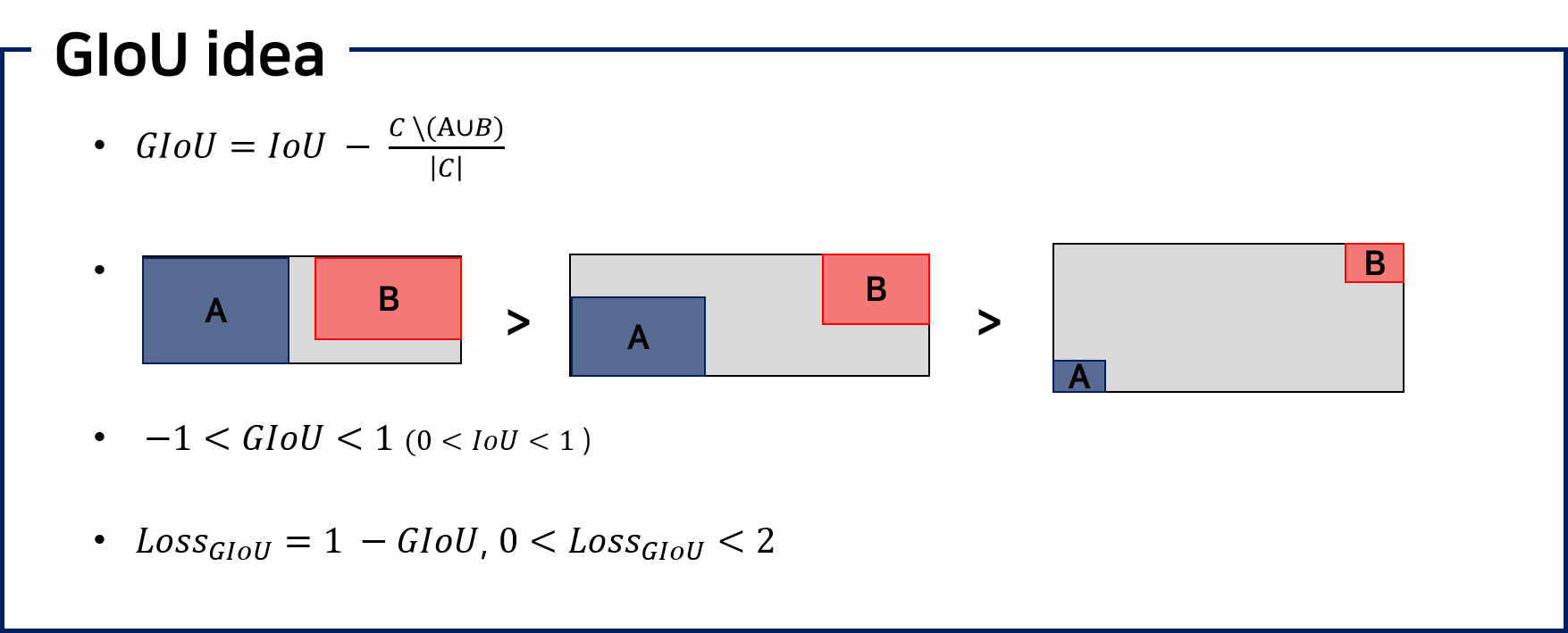
 A와 B 영역을 모두 감쌀 수 있는 최소 영역인 C를 만들고, C를 활용하여 A와 B가 얼마나 떨어져 있는지에 대해 반영할 수 있는 추가 항을 도입한다. 처음의 공식을 보면 기존 IoU에서 전체에서 회색 공간이 차지하는 비율을 뺀 값을 GIoU로 설정한 것을 볼 수 있다. 이 때문에 회색 공간의 비율이 IoU보다 크게되면 GIoU는 음수를 가질 수 있다는 특징이 있다.

 GIoU는 -1부터 1 사이의 값을 같게 된다는 것과 두 박스가 얼마나 떨어졌는지를 반영할 수 있다는 점이 기존 IoU와의 가장 큰 차별점이다. 하지만 두 박스가 완전히 겹친 경우(즉, 학습을 더이상 할 필요가 없는 경우) 1의 값을 가진다는 부분에서는 유사하다.

 저자가 처음 제시했던 Loss = 1 - IoU를 수정하여 Loss = 1 - GIoU로 설정하면 박스가 멀어져도 훈련이 가능하고, 박스가 겹친 경우 더이상 훈련되지 않는 시스템을 갖출 수 있다.

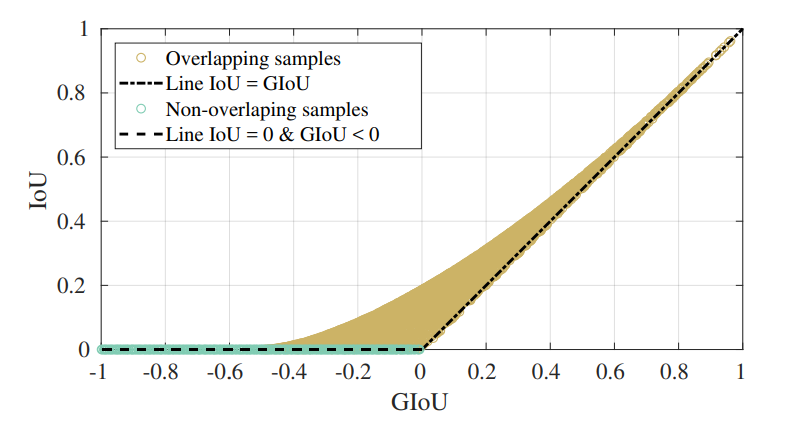
 그래프를 보면 초록색으로 표시된 부분(겹치지 않은 박스 샘플)의 IoU 값은 0으로 일정하지만, GIoU 값은 음수로서 계산되는 모습을 볼 수 있다. GIoU를 활용하면 이 부분에 찍힌 점들을 모두 학습 가능하다는 이야기.

4. Experimental Results

 실험 결과는 당연히 GIoU Loss를 활용했을 경우가 기존 MSE나 L1 smooth 를 활용한 경우보다 향상되었다. 이 논문에서는 YOLO v3, Faster R-CNN, Mask R-CNN에 대한 실험을 진행하였고, YOLO v3에선 상대적으로 큰 향상이 이루어졌다.(2014 validation set of MS COCO기준 AP75 9.78% 향상)

이는 R-CNN 계열에서 Anchor Box 개념을 도입하였고, 상대적으로 촘촘하고 정교한 앵커 박스들을 활용했기 때문으로 짐작한다.