[논문리뷰]Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression(DIoU/CIoU)

 

 

* 이 논문에서 주장하는 DIoU/CIoU는 각각 Distance-IoU/Complete-IoU의 줄임말이며, 바로 직전에 리뷰했던 GIoU의 아이디어에서 한 단계 더 발전한 논문이다.

* 중국의 텐진 대학에서 발표한 논문이며, 현재 21년 2월 18일 기준 96회의 인용수를 기록하였다.

---

1. Introduce

- 이전에 말했듯이 지금까지 대부분의 논문은 n-norm 손실을 활용해왔고, GIoU 논문에서는 이를 IoU로 대체하는 방식으로 기존 딥러닝 네트워크 성능을 향상시켰다.

(Generalized Intersection over Union: A Metric and A Loss for Bounding BoxRegression(GIoU) 참고)

- 하지만 이 GIoU는 수렴 속도가 느리고 부정확한 회귀를 한다는 문제점을 여전히 가지고 있다. 저자는 이를 해결하기 위해 DIoU를 제시한다.

GIoU의 수렴 과정

- 그림은 GIoU의 수렴 과정을 시각화 한 자료이며 검은 박스가 첫 Detection, 초록 박스가 수렴해야 할 Ground Truth, 파란 박스가 이전 과정에서 수렴한 박스(훈련 중인 박스)를 의미한다. 그림에서 볼 수 있듯이 GIoU의 수렴 속도를 느리게 하는 주요 원인은 박스의 수렴 방식에 있다. 박스는 Ground Truth로 이동하는 모습이 아니라, 박스를 키워 Ground Truth와 겹쳐진 후에 Ground Truth와 완전히 겹쳐지는 과정을 거친다. 여기서 박스의 위치와 스케일 수렴이 따로 이루어진다고 생각할 수 있다.(박스의 크기가 바뀌고 GT와 겹쳐지기까지의 과정이 Location 수렴이라고 생각하면 겹쳐진 후 박스의 크기와 중심을 GT에 맞추는 과정이 Scale 수렴이라고 볼 수 있다.)

DIoU의 수렴 과정

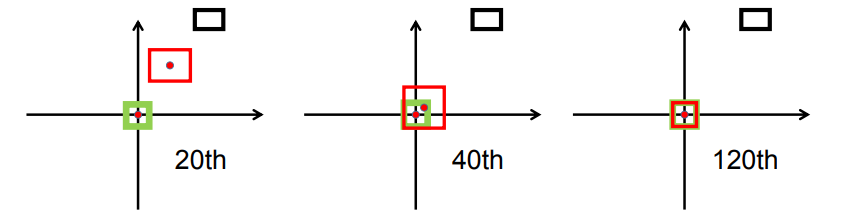
- 하지만 DIoU의 경우 박스 간의 거리(중심점 간의 거리) 역시 파라미터로 도입하여 Scale의 변화가 크지 않고 상대적으로 빠르게 Ground Truth와 겹쳐지는 모습을 보인다. GIoU의 경우 400회에도 완전히 수렴하지 못했지만, DIoU는 120회만에 BBOX가 수렴한 모습을 볼 수 있다.

케이스별 IoU/GIoU/DIoU 비교

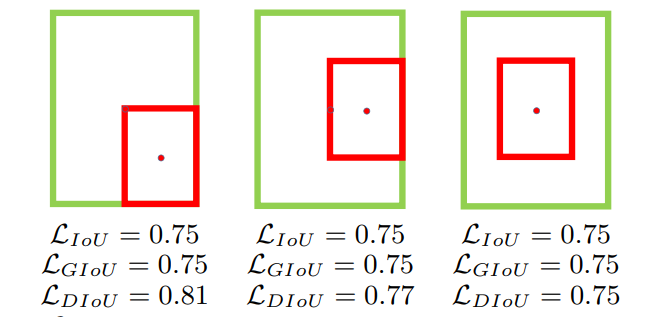
- 위의 그림이 수렴 속도를 느리게 하는 가장 큰 원인인데, 박스 두 개가 겹쳐있는 경우엔 GIoU에서 도입한 C 영역은 A와 B의 합집합의 크기와 같아지고, 결국 기존 IoU와 같은 값을 갖는다. 즉, 박스가 떨어져 있는 경우에 집중했던 GIoU는 박스가 겹쳐있는 경우까지는 고려하지 못한 방식이다.

- 이 논문에서는 중심점 간의 거리를 파라미터로 도입한 DIoU를 사용하였고, 위의 그림에서도 각각 다른 값을 갖는 모습을 보여준다.(여기서 세 번째 그림에서 DIoU 역시 완전히 수렴하지 않았음에도 IoU와 같아지는 문제를 보이는데 이는 뒤에 나올 CIoU로 해결이 가능하다.)

---

2. Related work

2.1 IoU와 GIoU의 Loss 분석

- 원래는 IoU의 손실과 원래는 IoU의 손실과 GIoU의 손실의 한계를 분석하는 것이 필요하다. 그러나 회귀 과정에선 다양한 다른 거리, 척도, 종횡비 등의 요소가 반영된다. 이러한 변인이 통제되지 않고 포괄적이지 않은 벤치마크의 회귀 과정의 경우, Detection 결과에서 BBOX 회귀 절차를 분석하는 것은 매우 어렵다.
이를 위해 저자는 회귀 사례를 종합적으로 고려하여 주어진 손실 함수의 문제점을 쉽게 분석할 수 있는 시뮬레이션 실험을 수행하였다.

 

2.2 Simulation

Simulation 구조, 1,715,000개의 시나리오가 존재

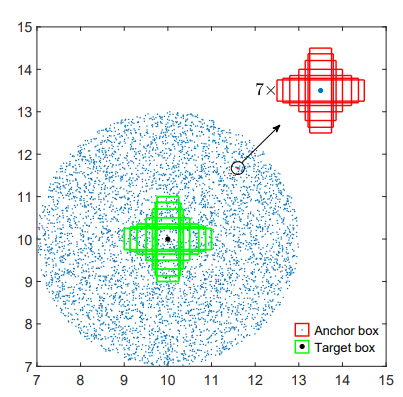
-이 실험에선 그림과 같이 거리, 스케일, 종횡비를 모두 고려하여 BBOX 간의 관계를 다룬다. 위의 그림을 참고하면 이해가 편하다.

 

〈Simulation 환경 구성〉

  1. 타겟 BBOX는 7개의 비율(1:4, 1:3, 1:2, 1:1, 2:1, 3:1, 4:1)을 갖고 넓이가 1인 앵커 박스를 가진다.
  2. 7개의 타겟 박스의 중심점은 (10,10)에 고정된다.
  3-1 거리: 앵커 박스는 5,000개의 지점에 균일하게 흩어져 있다.  
  3-2 배율: 각 점마다 존재하는 앵커 박스의 넓이는 0.5, 0.67, 0.75, 1, 1.33, 1.5, 2로 설정된다.  
  3-3 종횡비: 특정 점 및 배율에 대해 7가지의 종횡비를 사용한다.(이는 타겟 박스와 같다)  
  4. 모든 5,000x7x7개의 앵커 박스는 loss function에 의해 각각의 타겟 박스에 딱 맞도록 이동한다.

 요약하면, 시뮬레이션에는 1,715,000(7x7x7x5,000)개의 회귀 시나리오가 있다고 할 수 있다. 주어진 손실 함수 $L$에 의해 각각의 케이스에서 경사하강법(Gradient decent Algorithm) BBOX 회귀를 시뮬레이션 할 수 있다.

 

$B^t_i = B^{t-1}_i + \eta (2 - IoU^{t-1}_i)\nabla B^{t-1}_i$

 

 예측된 박스 \(B^t_i\)에서 $t$는 반복 횟수를 뜻하고, $\nabla B%{t-1}_i$는 $t-1$번째에 대한 기울기 손실을 의미하며 $\eta$는 step을 의미한다. 여기서 주목할만한 점은 $2 - IOU^{t-1}_i$를 기울기에 곱하여 수렴 속도를 더 빠르게 했다는 점이다.

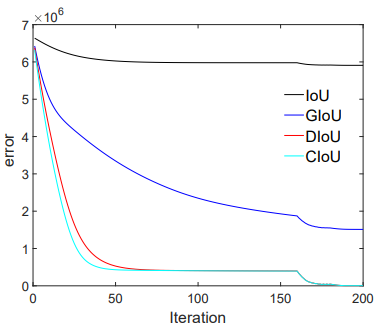
 BBOX 회귀는 $l_1-norm$에 의해 평가되며, 각각의 손실 함수를 사용한 시뮬레이션은 t=200까지 진행되었으며, error 그래프(Loss의 수렴 결과)는 위의 그림과 같다.

 

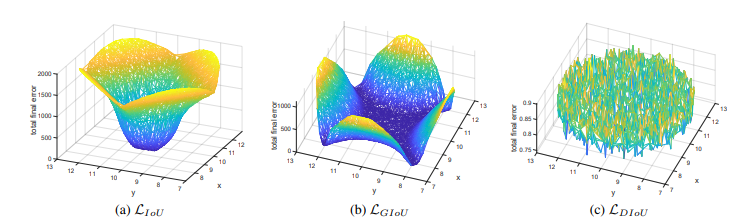
- 이 그림을 보면 IoU는 박스가 겹친 경우에만 수렴하는 모습을, GIoU는 모두 수렴은 하지만 그 속도가 느린 모습을 보인다. 하지만 DIoU의 경우는 빠르게 수렴하는 것을 볼 수 있다.

- 실제로 GIoU의 경우 $|C - A \cup B|$를 패널티로 활용하지만 그 넓이가 가끔 너무 작거나 0인 경우가 존재한다. 이런 케이스에선 GIoU의 영향력은 낮거나 없는 것과 같기 떄문에 수렴 속도가 매우 느린 모습을 보인다.

- 저자는 이 수렴 속도를 증가시키기 위하여 두 상자 간의 거리 값도 패널티로 주는 방향으로 설계된 DIoU를 제시하였고, 실제로 더 정확하고 빠른 회귀를 보였다.

---

3. 제안된 알고리즘(DIoU/CIoU)

3.1 Distance IoU

논문에서 제시한 DIoU 손실함수의 구조는 아래와 같다.

 

$\mathcal{L} = 1 - IoU + \mathcal{R}(B, B^{gt})$

 

- 여기서 1 - IoU 부분은 기존의 IoU를 활용한 손실 함수와 동일하고, $\mathcal{R}$로 묶인 항은 새롭게 정의된 패널티항으로 볼 수 있다. 이 부분은 GIoU와 DIoU, CIoU가 모두 다른데, DIoU의 경우, 아래와 같이 정의할 수 있다.

 

$\mathcal{L}_{DIoU} = 1 - IoU + \frac{\rho^2(b, b^{gt})}{c^2}$

 

- $\rho$는 유클리드 거리를 뜻하고, $b$와 $b^{gt}$는 BBOX들의 중점이다. c는 GIoU에서 정의한 두 박스를 최소의 크기로 감쌀 수 있는 C박스의 대각선 거리이다.(아래 그림 참고)

GT 박스와 Deteced 박스, 그리고 C박스

 

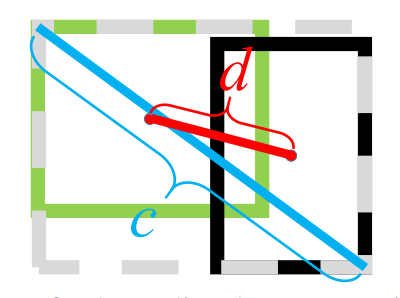
· DIoU의 특징은 다음과 같다.

1. 1. 스케일에 영향을 받지 않는다.
2. 2. GIoU와 비슷하게 박스가 겹치지 않아도 겹치도록 수렴한다.
3. 3. 두 박스가 완전히 겹쳤을 때는 $\mathcal{L}_{IoU} = \mathcal{L}_{GIoU} = \mathcal{L}_{DIoU} = 0$이고, 두 박스가 완전히 겹치지 않았을 때는 $\mathcal{L}_{GIoU} = \mathcal{L}_{DIoU} = 2$이다.
4. 4. 하지만 DIoU 손실은 박스가 겹치도록 빠르게 수렴하는 모습을 보인다.
5. 5. $|C - A \cup B| = 0$인 상황일 때도 GIoU와 달리 DIoU는 빠르게 수렴할 수 있다.

---

3.2 Complete IoU

그렇다면 Complete IoU(CIoU)란 무엇일까? CIoU는 아래와 같은 식으로 표현된다.

 

$\mathcal{R}_{CIoU} = \frac{\rho^2(b,b^{gt})}{c^2} + \alpha\upsilon$

 

$\alpha$는 trade-off 파라미터이고, $\upsilon$은 가로 세로의 비율의 연속성을 나타내는 파라미터이다.

 

$$ \upsilon = \frac{4}{\pi^2}(\arctan{\frac{\omega^{gt}}{h^{gt}}} - \arctan{\frac{\omega}{h}})^2 $$

 

또한, $\alpha$는 다음과 같이 정의되며 겹치는 영역의 값이 높은 우선순위를 갖게 하여, 겹치지 않았을 때 더 빠른 수렴을 가능하게 한다.

 

$\alpha = \frac{\upsilon}{(1 - IoU) + \upsilon}$,

 

최종적으로, 아래의 CIoU loss의 최적화 과정에서 활용되는 $h$와 $\omega$에 대한 $\upsilon$의 기울기 항을 제외하고는 DIoU와 같다.

$\frac{\partial\upsilon}{\partial\omega} = \frac{8}{\pi^2}(arctan\frac{\omega^{gt}}{h^{gt}} - arctan\frac{\omega}{h}) \times \frac{h}{\omega^2 + h^2}$,

 

$\frac{\partial\upsilon}{\partial h} = -\frac{8}{\pi^2}(arctan\frac{\omega^{gt}}{h^{gt}} - arctan\frac{\omega}{h}) \times \frac{\omega}{\omega^2 + h^2}$

 

여기서 $\omega$와 $h$ 값이 0과 1사이에 존재 할 때는 $\omega^2 + h^2$ 값이 너무 작아져서 기울기 폭발(gradient explosion)이 발생할 수 있다. 이를 방지하기 위하여 $\frac{1}{\omega^2 + h^2} = 1$로 대체하여 간단히 위험 요소를 제거할 수 있다. 이 작업을 거치더라도 기울기 수렴 방향은 불변한다.

---

3.3 Distance IoU를 접목시킨 Non-Maximum Suppression

- 이 아이디어는 NMS 알고리즘에도 접목시킬 수 있는데, 기존의 방식은 IoU를 활용하기 때문에 Occlusion(가림)이 발생한 경우에 올바른 박스가 삭제되는 문제가 발생한다. 이에 DIoU를 병합하는 것은 굉장히 간단하다. 기존 IoU로 점수를 계산하던 부분에 $\mathcal{R}_{DIoU}$항을 추가하면 되기 때문이다.

$$ s_i = \begin{cases} s_i, IoU - \mathcal{R}_{DIoU}(\mathcal{M},B_i) \lt \epsilon \\ 0, IoU - \mathcal{R}_{DIoU}(\mathcal{M},B_i) \geq \epsilon\\ \end{cases}\ $$

 

- $\epsilon$은 임계값이며, $s_i$는 분류 점수이다. 중심 거리가 멀면서 IoU가 큰 경우에는 다른 물체를 감지하였을 가능성이 있기 때문에 삭제하지 않는다. 이 방식은 코드로도 간단히 구현할 수 있다는 장점 역시 가지고 있다.

---

관련 코드

[Loss function] GIoU / DIoU / CIoU Matlab 코드

---

4. Reference

Zheng, Zhaohui, et al. "Distance-IoU loss: Faster and better learning for bounding box regression." Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 34. No. 07. 2020.