0.Abstract
- 딥러닝 네트워크는 높은 정확도를 위해 큰 연산 비용을 치룬다. 하지만 대다수의 사용자는 높은 정확도는 필요하지만 빠른 동작이 필수적이다.
- 이에 맞추어 Floating point으로 훈련된 최신 네트워크들을 Fixed point로 양자화하고 그 성능을 유지할 수 있다면 연산 속도가 빨라질 것이다.
- 제안된 PACT는 activation을 임의의 bit 정밀도로 양자화가 가능하며 일반적인 양자화보다 높은 정확도를 확보할 수 있다.
- 특히 가중치/활성화를 4bits 정밀도로 양자화할 수 있으며 성능은 Full precision과 유사한 동향을 보였다.
1. Primary Contribution:
- 최적 양자화 스케일을 찾을 수 있는 새로운 활성화 함수 양자화 기술인 PACT를 제안한다.
- 새롭게 도입한 α 파라미터는 활성화 함수를 클리핑하는 수준을 결정하기 위해 사용되며, 역전파를 통해 학습된다.
- α는 양자화 오류를 줄이기 위해 ReLU보다 Scale이 작으며, 경사 흐름을 원활히 만들기 위해 전통적인 클리핑 활성화 함수보단 Scale이 크다.
- 빠른 수렴을 위해 Loss function에서 α는 정규화된다.
- Extremely low bit-precision(≤ 2-bits for weights & activation)에서 PACT는 최고의 양자화 모델 정확도를 달성했다.
- PACT에 의해 양자화된 4-bit CNN은 single-precision floating point 모델과 비슷한 정확도를 달성하였다.
- 다양한 bits 표현에 따른 하드웨어 복잡도와 모델의 정확도의 Trade-off 관계를 입증하고 분석한다. 또한, PACT의 컴퓨터 엔진 관점에서의 엄청난 효과를 보일 수 있음을 보이고 시스템 레벨에서의 성능 향상을 확인한다.
2.Challenges in Activation Quantization
- 가중치 양자화는 가중치과 관련된 Loss function의 가설 공간을 이산화(discretizing)하는 것과 같다. 따라서 모델 훈련 중에 가중치 양자화 오류를 보상하는 것이 가능하다!
- 애석하게도 과거에 사용하던 활성화 함수는 훈련 가능한 파라미터를 가지고 있지 않았기 때문에 활성화를 양자화하면서 증가하는 에러를 역전파로 즉시 보상할 수 없었다.
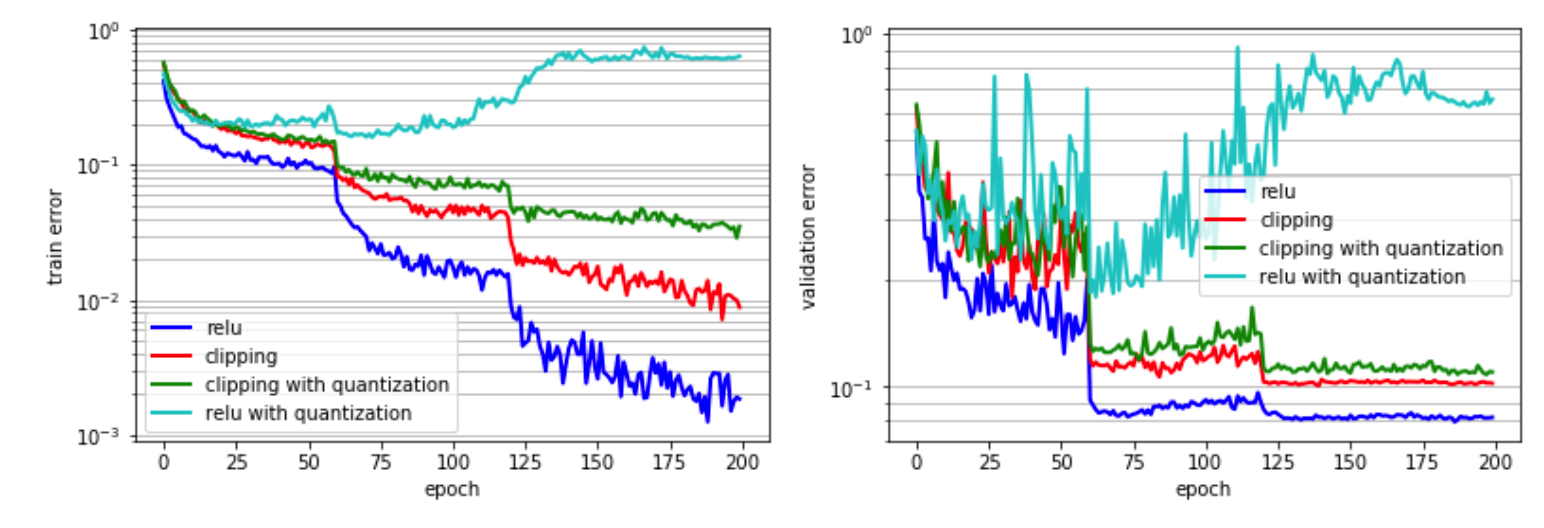
- 이와 달리 ReLU는 활성화 기울기를 파라미터로 전파하여 다른 활성화 함수에 비해 우수한 정확도를 달성하기 때문에 훈련할 파라미터를 보유하고 있다. 하지만 ReLU의 출력은 (0,∞)이므로 ReLU 이후의 양자화를 위해선 엄청난 동적 범위(ex. more bit-precision)가 요구됐다. 그림을 봐도 양자화된 relu의 성능이 매우 떨어짐을 확인할 수 있다.
- 이러한 동적 범위(High dynamic range) 문제는 threshold(upper bound)를 주는 방식인 clipping을 사용하여 어느정도 해결 가능하다. 하지만 레이어 마다, 모델마다 최적의 전역 Clipping 값을 결정하기 매우 어렵다. 그림을 확인해보면 clipping을 함께 활용했을 때 relu에 양자화를 적용했을 때보단 오류가 줄었지만 아직도 baseline 보단 오류가 큰 것을 확인할 수 있다.
3.PACT: Parameterized Clipping Activation Function
- PACT에서는 Clipping level을 설정하는 α가 존재한다. α는 양자화로 인해 발생한 정확도 감쇠를 줄이기 위한 목적으로 역전파를 통해 훈련 간에 동적으로 교정된다.
- 기존 사용하던 ReLU는 다음과 같은 함수로 교체된다:
$$y = PACT(x) = 0.5(|x| - |x - \alpha| + \alpha) = \begin{cases} 0, & \mbox{} x\in(-\infty,0)\\ x, & \mbox{} x\in[0,\alpha)\\ \alpha, & \mbox{} x\in[\alpha, +\infty) \ \end{cases}$$
- α는 활성화 함수의 범위를 제한하는 역할을 수행하며, 잘린 활성화 출력은 다음 수식으로 dot-product를 위해 k bits로 선형 양자화된다.
$$y_q = round(y\cdot \frac {2^k-1}{\alpha}) \cdot \frac {\alpha}{2^k -1}$$
- 위의 활성화 함수를 활용하면 α Loss functino의 변수이며 훈련 중에 값을 최적화할 수 있다. 역전파의 경우 ∂yq/∂α는 STE(Straight-Through Estimator)를 활용하여 계산되며 ∂yq/∂y를 1로 추정할 수 있다.
$$\frac{\partial y_q}{\partial\alpha} = \frac{\partial y_q}{\partial y}\frac{\partial y}{\partial\alpha} = \begin{cases} 0, & \mbox{} x \in (-\infty, \alpha) \\ 1, & \mbox{} x \in [\alpha, +\infty) \end{cases}$$
- α가 클수록 매개변수화 된 Clipping 함수가 ReLU와 비슷해진다. 넓은 동적 범위로 인한 큰 양자화 오류를 방지하기 위해여 α에 대해 L2-정규화를 적용한다. Fig2는 완전 정밀 훈련 간 초기값 10에서 시작했을 때 L2-정규화를 적용하면 α 값이 어떻게 변하는지 보여준다. 훈련 apoch에 따라 α가 훨씬 작은 값으로 수렴하여 활성화의 범위를 제한하고 손실을 최소화하는 것을 확인할 수 있다.

3.1. Understanding How Parameterized Clipping Works
- Fig.3은 사전 훈련된 SVHN 네트워크에서 α 범위에 대한 교체 엔트로피 및 훈련 소실을 보여준다.
- 모델에서 7개의 각 conv 레이어에 대한 활성화 함수 ReLU가 제안된 clipping ActFN으로 대체된 제안된 양자화 방식으로 훈련된다. 교차 엔트로피를 계산할 때는 현 레이어의 α를 제외한 모든 파라미터를 고정한 상태로 한 번에 한 레이어씩 α 값을 수정한다.
- 양자화 없이 계산된 교차 엔트로피는 Fig 3. (a)에 나와있다. 이는 α=∞와 같고, 교차 엔트로피는 α가 증가함에 따라 많은 레이어에서 작은 값으로 수렴된다는 사실을 확인할 수 있다. (ReLU는 좋은 활성화 함수임을 다시한 번 확인할 수 있다)
- 그러나 α를 훈련하면 특정 레이어에 대한 교차 엔트로피를 줄일 수 있을 것 역시 예상할 수 있다. act0과 act6의 그래프를 보면 튀는 모습을 보이기 때문이다.
- 다음으로 양자화 된 교차 엔트로피는 Fig3. (b)에 나와있다. 양자화를 사용하면 대부분 α가 증가함에 따라 교차 엔트로피가 증가하여 ReLU의 성능이 떨어짐을 볼 수 있다. 또한 최적의 α가 레이어마다 다른 것을 관찰할 수 있는데, 훈련을 통해 양자화 Scale을 학습한다면 해당 문제를 해결할 수 있을 것이다. 또한, 특정 범위에 대해 교차 엔트로피가 높은 엔트로피에 수렴(act6)하는 것을 확인할 수 있는데, 이는 경사하강법 기반 훈련에 문제를 일으킬 수 있다.
- 마지막으로, Fig 3. (c)에서는 교차 엔트로피와 α 정규화 학습을 모두 사용한 총 훈련 손실을 보여준다. 정규화는 훈련 손실의 안정화 수렴을 효과적으로 제거하여 경사하강법 기반 훈련에 효과적인 수렴을 일으킨다. 동시에 α 정규화는 전역 최소점을 확실하게 한다. 그림을 보면 훈련 손실 커브상의 최적 α 값에 점을 확인할 수 있다.

3.2. Exploration of Hyper-Prarmeters
3.2.1. Scope of α
저자는 총 세 가지 케이스를 비교하였다.
- 뉴런 활성화 별 개별적인 α 값
- 같은 출력 채널을 가지는 뉴런 사이에서 공유되는 α값
- 레이어에서 공유되는 α값
CIFAR10+ResNet20으로 실험한 결과 세 번째 케이스가 가장 높은 성능을 보였다. 이는 하드웨어 복잡도 측면에서도 레이어에서 Multiply-accumulate(MAC) 연산 이후 α가 한 번만 곱해지므로 더 좋은 결과를 보인다.

3.2.2. Initial Value and Regularization of α
- α가 매우 작은 값으로 초기화되면 더 많은 활성화가 0이 아닌 기울기 범위에 들어가, 훈련 초기에 불안정한 α값을 만들 가능성이 있고 정확도를 하락시킬 수 있다.
- 그렇다로 α가 매우 큰 값으로 초기화되면 기울기가 너무 작아지고 α가 큰 값으로 고정되어 잠재적으로 양자화 오류가 더 커질 수 있다.
- 따라서 넓은 동적 범위를 가지고 불안정한 α값을 피하기 위하여 적당히 큰 값으로 α를 초기화하고, 양자화 오류를 완화하기 위하여 α값을 정규화하는 작업이 필요하다.
- 실제로 α에 대해 L2-정규화를 적용할 때 계수 가중치를 α에도 동일하게 적용할 수 있다. Fig. 8을 보면 PACT 양자화 검증 오류가 넓은 범위의 가중치(λ) 값에 대해 크게 별화지 않는 것을 확인할 수 있다.

4. Experiment

- 그림을 보면 training/validation error가 full-precision과 비슷하다는 것을 확인할 수 있다.

- 또한, 표에서 볼 수 있듯이 DoReFa와 비교했을 때 더 높은 성능을 보였으며, 4bits 양자화를 PACT로 수행했을 때, full-precision과 성능이 비슷하거나 심지어 더 좋게 나온 케이스도 존재했다.
- 중요한 것은 가장 낮은 bit 정확도에서도 full-precision 대비 1% 이하의 성능 하락만이 발생했다는 점이다.